写在前面
研二下做的文本分析不做了,转战机器学习人脸识别(老板要求发高质量高水平的文章),没接触过这个领域,不知道自己可以做到什么程度,这次有靠谱学长指导总是很欣慰的(比起之前小老师出去创业只能自己瞎鼓捣好太多了)。
Day 2017/10/18: 学长推荐入门阅读 Robust Face Recognition via Sparse Representation
说实话自己英文阅读水平很一般,而且线性代数学的那些知识基本都还给老师了,这篇论文看的着实心累。再加上自己很反感写论文,看的进度很慢,基本看几个词就走神的那种。在此特别特别特别感谢@超哥的耐心讲解。
学长说不用非得看明白推导,但是需要了解算法的过程。而且看论文要养成习惯,把比较好的英文词语、短语、比较学术的词都整理记录下来方便以后用,这个很重要。
预备知识
我们想要描述向量 $\vec x = (x_1, x_2)$ 的长度,那么用什么来度量?
$$
模 \Leftrightarrow 范数 \Leftrightarrow 长度
$$
$\ell^2$ 范数就是我们通常意义上的模,即欧氏距离:$||\vec x||_2 = \sqrt{\sum_{i=1}^Nx_i^2} = x_1^2 + x_2^2$ 。二维空间 $\ell^2$ 范数对应的曲线是圆,在三维空间 $\ell^2$ 范数就是球体。
$\ell^1$ 范数即:$||\vec x||_1 = \sum_{i=1}^N|x_i|$ 即向量元素绝对值之和。
$\ell^0$ 范数指 $\vec x$ 中非0元素的个数。
范数对应的曲线如图:
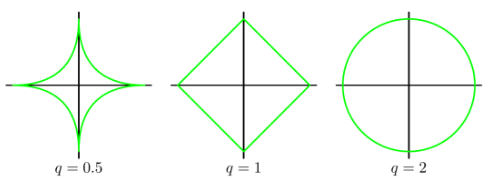
论文思想
给定 $k$ 类样本集,每一类是同一个人的多张图片,将每张图片(是一个像素为 $w \times h$ 的矩阵)按照列堆砌表示成 $m$ 维向量形式 $\vec v \in R^m (m=wh)$,那么给定的 $n_i$ 个第 $i$ 类的训练样本可以表示为矩阵 $ A_i = [\vec v_{i,1}, \vec v_{i,2}, \dots, \vec v_{i,n_i}] \in R^{m \times n_i} $ 。
整个训练集可以表示为:
$$
A = [A_1, A_2, \dots, A_k] = [\vec v_{1,1}, \vec v_{1,2}, \dots, \vec v_{k,n_k}]. \tag{1}
$$
给定测试样本图像 $\vec y \in R^m$,假设是属于第 $i$ 类的,那么可以根据第 $i$ 类样本线性表示如下:
$$
\vec y = \alpha_{i,1} \vec v_{i,1} + \alpha_{i,2} \vec v_{i,2} + \cdots + \alpha_{i,n_i} \vec v_{i,n_i}, \tag{2}
$$
$$
\vec y = ( \vec v_{i,1}, \vec v_{i,2}, \cdots, \vec v_{i,n_i}) (\alpha_{i,1}, \alpha_{i,2}, \cdots, \alpha_{i,n_i})^T \tag{3}
$$
那么 $\vec y$ 的线性表示可以写为:
$$
\vec y = A\vec x_0 \in R^m. \tag{4}
$$
其中 $\vec x_0 = [0, \cdots, 0, \alpha_{i,1}, \alpha_{i,2}, 0, \cdots, 0]^T \in R^n$。
我们希望能够求解线性方程组 $\vec y = A \vec x$,其中未知数有n个,方程个数有m个。对于 $m < n$ 的情况,方程组是超定的$overdetermied$,存在这样的 $\vec x_0$ 是唯一解。对于人脸识别,给定的样本集很大,所以是 $m < n$ 的情况,这时方程组是欠定的$underdetermined$,解不唯一。一般解决这种问题是通过添加约束,取 $\ell^2$ 范数最小值:
$$
\begin{equation}
\begin{split}
\ell^2 &\quad\quad \hat{\vec x^ 2} = arg min ||\vec x||_2 \newline
\ s.t. &\quad\quad A\vec x = \vec y
\end{split}
\end{equation} \tag {5}
$$
$\ell^2$ 求解得到的 $\hat{\vec x_2}$ 是密集解,即有大量非0值。我们希望得到的解是稀疏的,也就是与第 $i$ 类有关的系数都为非0,无关系数都为0。最优的方式是求解 $\ell^0$ 范数,然而这个求解问题是NP-Hard:
$$
\begin{equation}
\begin{split}
\ell^0 &\quad \hat{\vec x^ 0} = arg min ||\vec x||_0 \newline
s.t. &\quad A\vec x = \vec y
\end{split}
\end{equation} \tag {6}
$$
$\ell^0$ 范数很难优化求解, $\ell^1$ 范数是 $\ell^0$ 范数的最优凸近似,而且更容易优化求解,所以该篇文章通过求解 $\ell^1$最小值问题来做稀疏表示。
$$
\begin{equation}
\begin{split}
\ell^1 &\quad \hat{\vec x^ 1} = arg min ||\vec x||_1 \newline
s.t. &\quad A\vec x = \vec y
\end{split}
\end{equation} \tag {7}
$$
几何解释
为什么 $\ell^1$ 范数比 $\ell^2$ 范数更容易得到稀疏解?
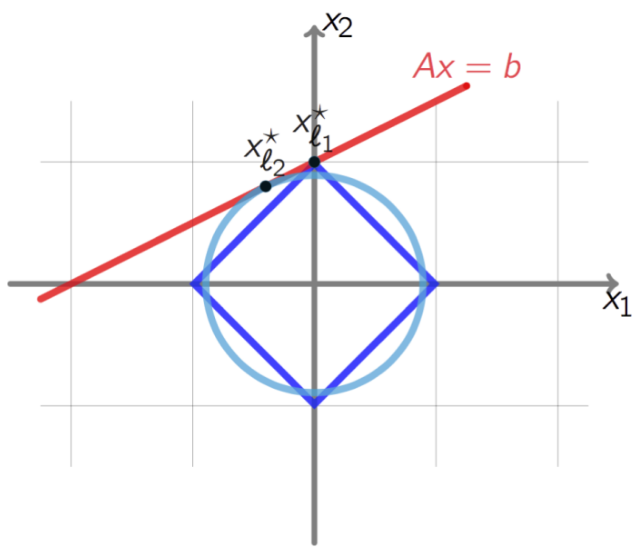
如图 $\ell^2$ 范数曲线在 $scale$ 过程中总会 $touch$ 到直线,得到的相切的点更大概率不在坐标轴上,也就是不稀疏。而 $\ell^1$ 范数曲线与直线相切的点更容易落在坐标轴上,这样的解是稀疏解,那么得到稠密解只有两种情况就是直线的斜率为 $1$ 和 $-1$ 的是时候,所以 $\ell^1$ 求得稀疏解的概率更大。
线性变换包括平移、旋转和缩放。$\vec y = A \vec x$ 求解方程中矩阵A作用域向量 $\vec x$ 相当于对向量进行线性变换,也就是将 $n$ 维的 $\vec x$ 映射到了 $m$ 维空间中。
定义单位 $\ell^1-ball \quad P_1$,在进行线性映射后 $\vec y = A \vec x$ 的求解问题落在了多面体 $P = A(P_1)$上。
噪音处理
$\vec y = A \vec x_0$ 是最精确理想的情况,实际上一定会存在噪音 $\vec y = A \vec x_0 + \vec z$,假设我们允许的误差范围是 $||\vec z||_2 < \varepsilon$ ,那么求解问题变为:
$$
\begin{equation}
\begin{split}
\ell_s^1 &\quad \hat{\vec x^ 1} = arg min ||\vec x||_1 \newline
s.t. &\quad ||A \vec x - \vec y||_2 \le \varepsilon
\end{split}
\end{equation} \tag {8}
$$
Algorithm 1
输入 $k$ 类训练样本 $A = [A_1, A_2, \dots, A_k] \in R^{m \times n}$,一个测试样本 $\vec y \in R^m$.
将A进行归一化。$\frac{\vec x}{||\vec x||_1} \to ||\frac{\vec x}{||\vec x||_1}||_1 = ||\frac{\vec x}{|x_1| + |x_2|}|| = \frac{||x_1|| + ||x_2||}{||x_1|| + ||x_2||} = 1$
求解 $\ell^1$最小化问题:
$$
\begin{equation}
\begin{split}
\ell^1 &\quad \hat{\vec x^ 1} = arg min ||\vec x||_1 \newline
s.t. &\quad A\vec x = \vec y
\end{split}
\end{equation} \tag{7}
$$计算残差:
$$
\begin{equation}
\begin{split}
\hat{\vec y} & = A {\hat{\vec x^ 1}} \newline
r_i(\vec y) & = ||\vec y - A \hat{\vec y}||_2
\end{split}
\end{equation} \tag{9}
$$
- 残差取最小得到 $\vec y$ 属于哪一类,$identity(\vec y) = arg min_i r_i(\vec y) $.
论文还讨论了两个问题
Feature Extraction
特征提取对于人脸识别的稀疏表示可以起到降低数据维度、减少计算开销的作用。比如图像分辨率为 $640 \times 480$ ,维数m在 $10^5$ 量级,这样采用上述 $Algorithm 1$ 过程计算会很慢很慢。所以将图像空间映射到特征空间 $R \in R^{d \times m}$ 其中 $d \ll m$ :
$$
\tilde{y} \doteq R \vec y = RA \vec x_0 \in R^d \tag{10}
$$
求解问题变为:
$$
\begin{equation}
\begin{split}
\ell_r^1 &\quad \hat{\vec x^ 1} = arg min ||\vec x||_1 \newline
s.t. &\quad ||RA\vec x - \vec y||_2 \leq \varepsilon
\end{split}
\end{equation} \tag {11}
$$
当特征维数 $d$ 满足 $d \geq 2tlog(n/d)$ 时,$Algorithm 1$ 能够快速迭代收敛,特征的选取不再是决定性的,即使是随机的映射或者降采样也可以表现的很好。
Robustness to Occlusion or Corruption
实际情形中会有被遮挡或者质量不好的测试样本 $\vec y$ ,需要将线性模型改写为:
$$
\vec y = \vec y_0 + \vec e_0 = A \vec x_0 + \vec e_0 = [A, I][\vec x_0, \vec e_0]^T = B \vec w_0 \tag{12}
$$
其中 $\vec e_0 \in R^m$ 是非零错误向量,求解问题变为:
$$
\begin{equation}
\begin{split}
\ell_e^1 &\quad \hat{\vec w^ 1} = arg min ||\vec w||_1 \newline
s.t. &\quad B \vec w = \vec y
\end{split}
\end{equation} \tag {13}
$$
算法过程和 $Algorithm 1$ 一致。
写在后面
为了能在hexo里正确显示latex语法,试了各种markdown renderer for hexo,总是个别语法有问题,鼓捣了老半天。。。必须贴一下这篇博文,至少是好使了,我勒个去。。。
其实看的稀里糊涂,真的是只知道了大概的算法过程,不过也算是有点收获。接下来开始学习线性降维PCA,加油啦~(≧▽≦)/~
