写在前面
最近恶补了线性代数的知识,大一时《线性代数》的课本居然一直留着,惊讶到我了,因为本科毕业时把所有课本都卖了,不知怎么想的唯独没卖《线性代数》这本书,当时居然知道三年后自己会用到,感觉好神奇😄。特别推荐一下马同学高等数学公众号以及感谢@大壮学长的讲解。
降维
高维数据意味着需要超过两个或三个维度来表示数据,在高维情形下出现的数据样本稀疏、距离计算困难等问题,是所有机器学习方法共同面对的严重障碍,称为“维数灾难”。
缓解维数灾难的重要途径是降维,即通过某种数学变换将原始高维属性空间转为一个低维子空间,在这个子空间中样本密度大幅提高,距离计算也变得更为容易。为什么能降维呢?因为很多时候,观测或收集到数据样本虽然是高维的,但与学习任务相关的也许仅是某个低维分布,即高维空间中的一个低维嵌入(embedding)。
基于线性变换来进行降维的方法称为线性降维方法,如PCA(Principal Component Analysis)、LDA(Linear Discriminant Analysis)。PCA降维原则是投影后数据尽可能分散即方差大,希望方差大的方向上数据无关即协方差为0,但PCA不一定有助于数据分类。LDA的降维原理是使降维后数据间类内距离尽可能小,类间距离尽可能大,是带标签的降维方法。
其实不同的降维方法就是保持了低维不同的样本相关性。
很多时候我们不知道数据的具体特征(高维信息),而仅仅知道数据与数据之间的相似程度。这种情况下对数据降维,必然要尽可能保证原来相似的数据在降维后的空间中依然相似,不相似的数据还是距离很远。解决这类问题通常采用非线性降维方法(Nonlinear Dimensionality Reduction):LE(Laplacian Eigenmaps)、LLE(Locally-linear embedding)。
LE
LE 和 LLE 都是从图的角度去构建数据之间的关系,图中每个点代表一个数据,每一条边权重代表数据之间的相似程度,越相似权值越大,并且它们都假设数据具有局部结构性质。LE假设每一个点都只与它距离最近的点相似,远的数据相似度为0,降维后相近的点仍保持相近。
设 $y_i \in R^{d \times 1}$ 是样本 $i$ 在低维(降到 $d$ 维)子空间中的向量表示,$w_{ij}$ 是点 $i$ 和 $j$ ( $j$ 为 $i$ 的 $k$ 近邻)之间的权重值。希望能够使降维后样本 $k$ 近邻两点之间距离越小,$w$ 越大则越相似,则要优化的目标函数为
$$
\sum_{ij} (y_i - y_j)^2 w_{ij}
$$
将目标函数展开,先看 $\sum_{ij} y_i^2 w_{ij}$ ,遍历 $j$ 则有 $D_i = \sum_j w_{ij}$
$$
\sum_{ij} y_i^2 w_{ij}
= \sum_{ij} y_i^2 \sum_j w_{ij}
= \sum_i y_i^2 D_i
= \sum_i y_i D_i y_i^T
= tr(Y D Y^T)
$$
其中 $Y = (y_{j1}, y_{j2}, \dots, y_{jk}) \in R^{d \times k}$,填充0至 $R^{d \times n}$,其中 $D$ 为对角阵:
$$
\begin {pmatrix}
D_1 & & & 0 \\
& D_2 \\
& & \ddots \\
0 & & & D_n
\end {pmatrix}
$$
$y_i D_i y_i^T$ 是 $Y D Y^T$ 对角线上的元素,所以转为求迹(trace)。
再看 $\sum_{ij} y_i y_j w_{ij} = tr(Y W Y^T)$,其中矩阵 $W \in R^{n \times n}$ 是样本相似度矩阵,这个相似度怎么度量,可以自由定,比如高斯核函数 $w_{ij} = exp(-||x_i - x_j||^2 / t)$ ,样本点之间距离越小,$w$ 值越大也就越相似。一般为了让样本点 $i$ 和 $j$ 互相在彼此的邻域内,做此处理 $W = \frac{W + W^T}{2}$ 。
有拉普拉斯矩阵 $L = D - W$,所以目标函数变为:
$$
\begin{equation}
\begin{split}
arg min \quad tr(Y^T L T) \newline
s.t. \quad Y D Y^T = I
\end{split}
\end{equation} \tag {1}
$$
LLE
LLE假设样本点可以由 $k$ 近邻的样本点线性表示,并且投影前后线性关系权重系数不变。
LLE的算法步骤为:
找每个样本点的 $k$ 个近邻点
由每个样本点的近邻点计算该样本点的局部重建权值矩阵
计算样本点的降维表示
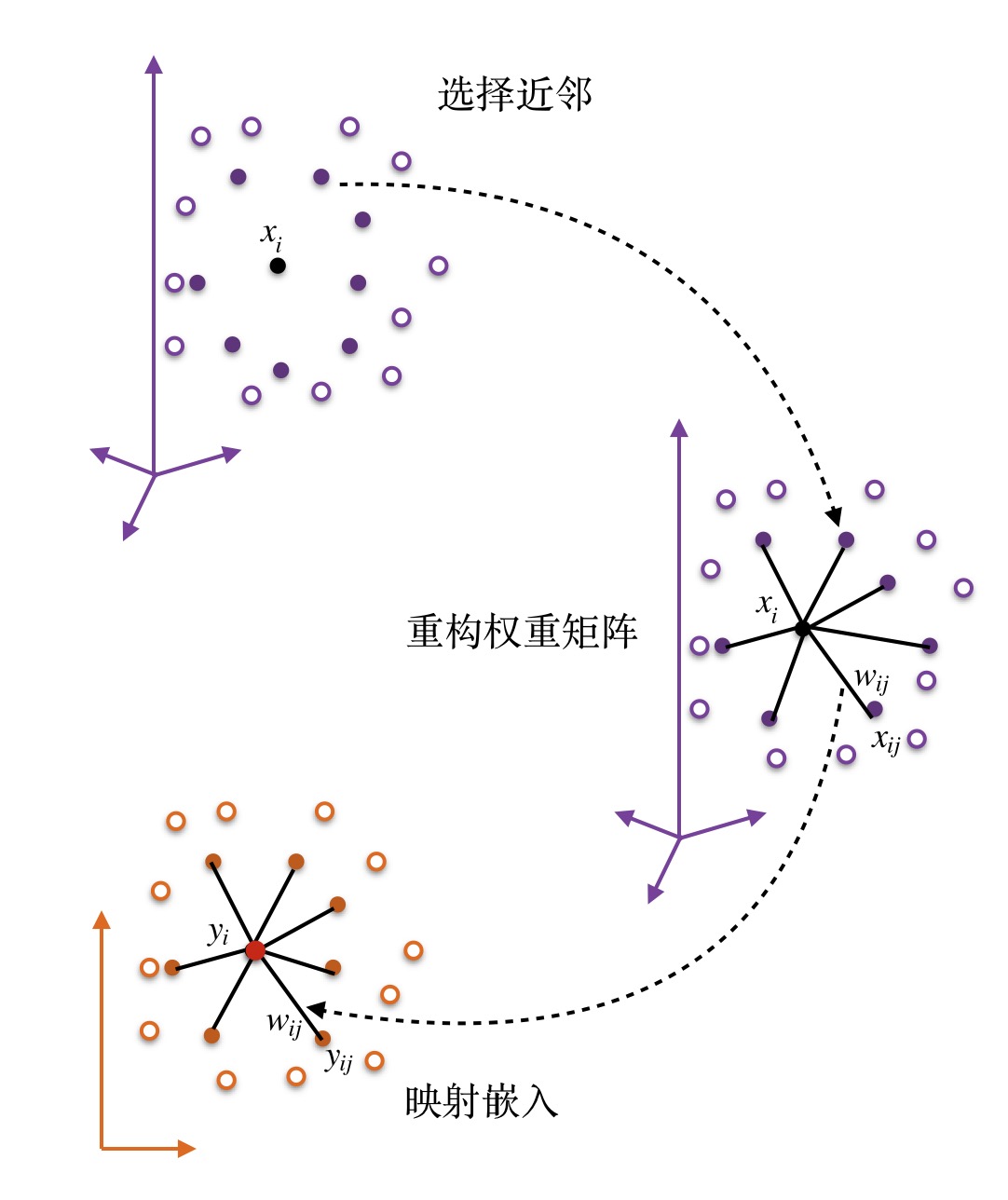
我们希望能够通过 $k$ 近邻的样本点来线性重构原样本点,定义误差函数为
$$
min \sum_i^n ||x_i - \sum_j^k w_{ij} x_{ij}||^2
$$
其中 $x_{ij} (j = 1,2,\dots,k)$ 是 $x_i$ 的 $k$ 个近邻点;$w_{ij}$ 是 $x_i$ 和 $x_j$ 之间的权值,满足 $\sum_j^k w_{ij} = 1$。
求解重构权重矩阵
$$
\begin{split}
||x_i - \sum_k^k w_{ij} x_{ij}||^2 =& ||\sum_j^k w_{ij} x_i - \sum_j^k w_{ij} x_{ij}||^2 \newline
=& \sum_j^k ||(x_i - x_j) w_{ij}||^2 \newline
=& \sum_j^k w_{ij}^T (x_i - x_j)^T (x_i - x_j) w_{ij} \newline
=& tr(W_i^T (X_i - X_j)^T (X_i - X_j) W_i)
\end{split}
$$
其中 $W_i = (W_{i1}, W_{i2}, \dots, W_{ik})^T \in R^{k \times 1}$, $X_j = (X_{j1}, X_{j2}, \dots, X_{jk})$, $X_i = (X_i, X_i, \dots, X_i) \in R^{D \times k}$。
令 $Z_i = (X_i - X_j)^T (X_i - X_j)$,有 $\sum_j^k w_{ij} = W_i^T I_k = 1$, $I_k$ 是 $k$ 维的全1向量。通过拉格朗日乘子法(Lagrange Multiplier)求解带约束的目标函数,构造拉格朗日函数:
$$
L(\alpha, \lambda) = W_i^T Z_i W_i + \lambda(W_i^T I_k - 1)
$$
由 $\frac{\partial L}{\partial W} = 0$ 得 $W_i = - \lambda Z_i^{-1} I_k/2$,再加上约束条件,则结果为:
$$
W_i = \frac{Z_i^{-1} I_k}{I_k^T Z_i^{-1} I_k}
$$
比如向量 $(2,3,4,5)^T$ 要想满足求和为1,则 $(2/14, 3/14, 4/14, 5/14)^T$, 即 $(1,1, \dots, 1)(2,3,4,5)^T$。
求解低维表示
根据原始空间 $k$ 近邻表示求得权重矩阵 $W_i$,LLE假设降维后低维空间中样本点之间仍然保持一致的线性关系,设低维表示为 $y_i \in R^{d \times 1}$,则低维目标函数为:
$$
min \sum_i^n ||y_i - \sum_j^k w_{ij} y_j||^2
$$
其中 $W_i = \sum_j^k w_{ij} \in R^{k \times 1}$填充0至 $R^{n \times 1}$,
$Y = (y_{1}, y_{2}, \dots, y_{d}) \in R^{d \times n}$
$y_i = Y1_i$,$1_i = (0, \dots, 1, \dots, 0)^T$ 是只有第 $i$ 位为1的 $R^{n \times 1}$ 的列向量
则:
$$
\begin{split}
\sum_i^n ||y_i - \sum_j^k w_{ij} y_j||^2 =& \sum_i^n ||Y1_i - YW_i||^2 \newline
=& Q_1^TQ_1 + Q_2^TQ_2 + \cdots + Q_n^TQ_n \quad//Q_i = Y1_i - YW_i \newline
=& tr(Y(I-W)(I-W)^TY^T)
\end{split}
$$
其中 $Q_i^TQ_i$ 恰好是 $(YI-YW)^2$ 对角线上的元素。
则令 $M = (I-W)(I-W)^T$ 优化目标函数为:
$$
\begin{equation}
\begin{split}
& argmin \quad tr(YMY^T) \newline
& s.t. \quad \sum_i^n y_i = 0 \newline
& s.t. \quad \frac{1}{n} \sum_i^n y_i y_i^T = I
\end{split}
\end{equation} \tag {2}
$$
通过拉格朗日乘子法求解,问题变为 $MY = \lambda Y$, 求矩阵 $M$ 最小的 $d$ 个特征值对应的 $d$ 个特征向量组成的 $Y = (y_1, y_2, \dots, y_d)$,最小的特征值0不能反映数据特征,通常选取第 $2 \sim d+1$ 个。
有关约束条件
因为低维表示 $y$ 有平移不变性,即通过加减常数进行平移,所以通过约束 $\sum_i^n y_i = 0$ 将低维表示限制在原点范围内。正交约束是因为希望降维后任何一维都不能通过其他维表示得到。
